What does it do?
This is pretty straight forward, just like normal convolution operation, it converts a piece of data structured [channels, height, width] to [kernal\_numbers, same\_height, same\_width], using a set of learn-able parameters in the size of [kernel\_number, channel\_number, weight\_for\_this\_channel]. This operation is usually just a meaningless scaling by a constant unless it is performed across channels, which is usually called a cascade cross channel pooling layer.
What's the purpose?
Along all materials read, it seems like this operation is widely used on the following purposes:
Dimension augmentation/reduction.
This operation is capable of mapping an input of any channel to an output of any channel while preserving the original size of the picture. Do be aware that such operation, especially in dimensionality augmentations, uses large amount of extra parameters, making the network possible more prone to overfitting.
Rescaling the last layer.
In the above it's mentioned that 1x1 convolution could serve as a plain scale of a whole channel, which is usually unnecessary. However, if such need exist, it could be met though this operation.
Increasing non-linearity.
The fact that it involves a non-linear mapping without drastically altering the input, the non-linearity of the network is increased without using plain fully-connected layers which destroys the relationship between nearby pixels. At the same time, the original size of the input could be preserved.
The (Network in Network)NIN Structure
This concept first appeared to me while reading a research paper called network in network, which seems to be another powerful modification made on CNNs. One of the key aspect this paper adapted is using a multilayer perceptron model to replace the traditional convolution kernel.
As I wonder how could this model be implemented using higher level api of popular machine learning libraries without modifying the lower level codes, the paper actually stated that such operation of sliding a mini-MLP over a picture across the previous channels is equivalent to cross channel convolution with 1x1 kernels, where a few new 1x1 convolutional layer(CCCP) is appended to a normal convolutional layer to reach the goal.
The fact that this CCCP operation appending to a normal convolution layers will make a equivalent MLP serves as a sliding convolution kernel, is hard to imagine to be true. It creates confusion in my understanding and it is not until I unroll the whole process so it could be under stood.
Rather than 2d convolution, using 1d convolution makes things more straight forward while the same rule applies to arbitrary dimensions of convolution.
Suppose we have an 1d input with 2 channels:

And we perform a normal convolution with one kernel of 2.

After appending a 1x1(in 1d convolution, just 1) convolution layer with two kernels, it looks like:

And another 1x1 layer with two kernels added:

It's not hard to see, that this structure is indeed a sliding MLP layer with the input size of the convolution size of the layer appended to, the depth of the number of 1x1 layers appended and the hidden unit numbers of the product of all kernel numbers in the hidden unit, the input numbers and the last layer.
The Inception module
The inception module is first used in the googlenet architecture, and proved to be really useful.
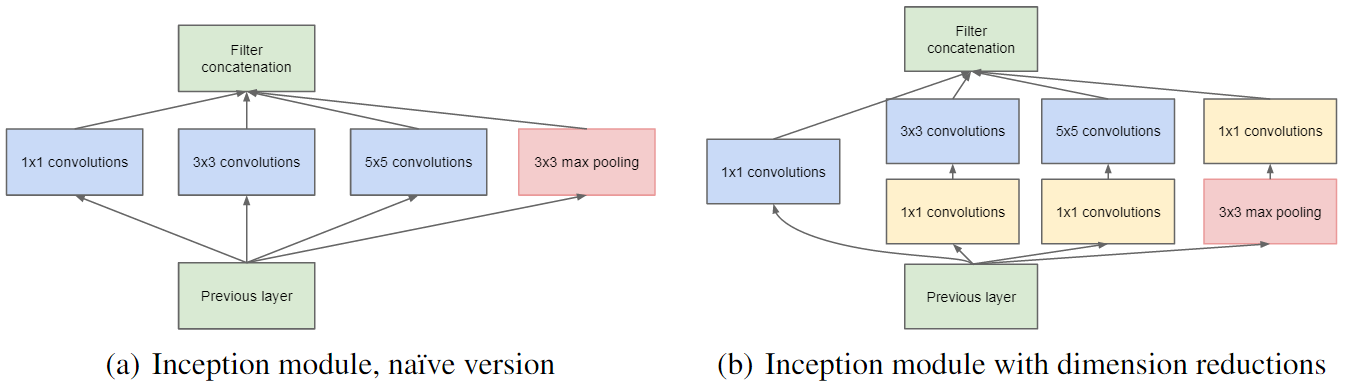
What this module does is really just adjoining all the output of different size of convolution/pooling together and let the network to choose which to use itself. The pro of this method is that the network is made more resistant to shift in sizes of the target, and the manually adjusting size of the kernels is no longer required--we got most of the possible sizes needed all here.
As a result, the 1x1 convolution naturally became one of the choices.
Ideas for Future Research
As I read, neurons that fired together creates a relationship between each other and every one of them got easier to fire next time given the condition that the related neurons are fired.
I am thinking that neurons in regular DNNs does not have any knowledge of the state of other neurons in the same layer, thus maybe it would be possible to create such a relation, to somehow create "logic" for networks?
To do so, maybe we need another set of weights in each neuron used to scale the states of other neurons in the same layer and add to the output, somehow like this: $$~$ \vec{y_{n}}=(\mathbf{W_n}^T \times \vec{y_{n-1}} + \vec{b_n})+\mathbf{W_{new}}^T (\mathbf{W_n}^T \times \vec{y_{n-1}} + \vec{b_n}) $~$$
n*n matrix considering n as the size of the output.
The detailed implementation is to be researched.
Edit: Okay… This seems to be just an really stupid way of adding an extra layer, and won't really make any difference from just adding one at all.(2017/10/27)
References:
http://blog.csdn.net/yiliang_/article/details/60468655
http://blog.csdn.net/mounty_fsc/article/details/51746111
http://jntsai.blogspot.com/2015/03/paper-summary-network-in-network-deep.html
https://www.zhihu.com/question/64098749